Mixing in T-Junctions: Momentum Ratios, Vortices, and Design Insights

Published on: September 8, 2025

Why T-Junctions Matter

The humble T-junction is everywhere: in chemical plants, natural gas pipelines, and even microfluidic devices.
At first glance, it’s just a side pipe feeding into a main line. But in reality, a T-junction is a canonical jet-in-crossflow (JICF) problem - one of the most studied yet still rich flow physics cases in fluid dynamics.

When a branch jet enters a main crossflow, the resulting interaction spawns a series of vortical structures, turbulent cascades, and scalar transport processes that dictate mixing efficiency.

Defining the Momentum Ratio

In most of the literature, the momentum flux ratio is defined as jet momentum ÷ crossflow momentum.
Here, I flip that definition to emphasize the competition between the crossflow and the branch jet:

\[J = \frac{\rho_\text{cross} U_\text{cross}^2}{\rho_\text{jet} U_\text{jet}^2}\]

Low (J): jet dominates (strong penetration).
High (J): crossflow dominates (jet bends, attaches to wall).

This framing makes the physics of a T-junction a momentum tug-of-war between crossflow and branch jet.

Flow Physics: The Vortices That Do the Work

Experiments using PIV and PLIF (Pan et al., 2001) and LES simulations (Salewski et al., 2008) reveal that a handful of coherent structures dominate mixing:

Counter-Rotating Vortex Pair (CVP): the kidney-shaped signature of JICF. The CVP folds the scalar interface, entrains crossflow into the jet, and drives macro-mixing.
Shear-Layer Vortices: Kelvin–Helmholtz instabilities at the jet edge — critical for near-field entrainment.
Horseshoe and Wake Vortices: wrap around the jet base and trail downstream, adding unsteadiness and small-scale stirring (Zhang & Yang, 2017).

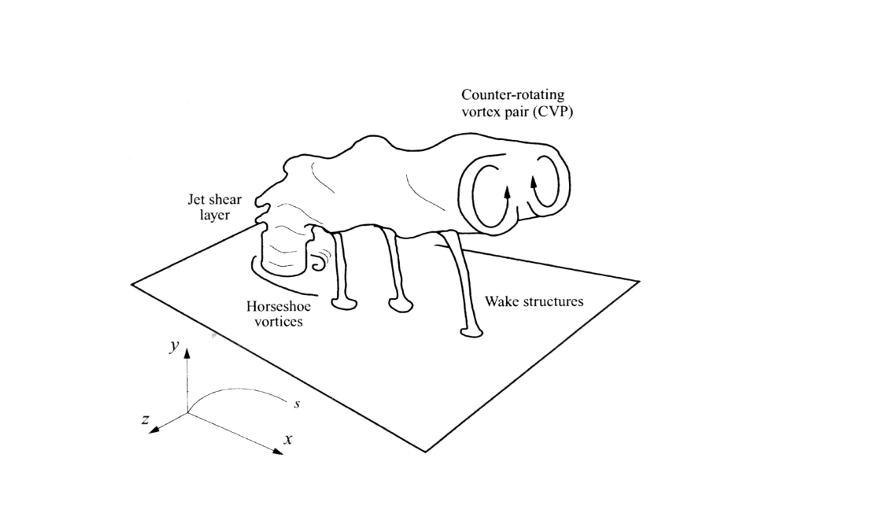
Key structures

Figure 1: Schematic from presentation showing CVP, shear-layer vortices, and horseshoe vortices around the branch jet.

Flow Regimes vs. Momentum Balance

Classic experiments by Kok & van der Wal (1996) (Kok & van der Wal, 1996) revealed three distinct flow regimes that arise from the competition between the branch jet and the main crossflow. In their study, the momentum ratio was defined as :

\[M_R = \frac{\rho_\text{jet} U_\text{jet}^2}{\rho_\text{main} U_\text{main}^2}\]

where higher Mr corresponds to a stronger jet. In this post, I use the inverse convention,

$J = \frac{\rho_\text{cross} U_\text{cross}^2}{\rho_\text{jet} U_\text{jet}^2} = \frac{1}{M_R}$ so that increasing J indicates a stronger crossflow (and weaker jet).

Figure 2 below, adapted from Kok & van der Wal (1996), shows the three canonical regimes as observed experimentally:

Wall-Jet Regime (high J, low $M_R$) – the crossflow dominates, bending the jet and causing it to attach to the wall downstream.

Deflected-Jet Regime (moderate J, moderate $M_R$) – the jet partially penetrates, forming a counter-rotating vortex pair (CVP) that drives efficient mixing.

Impinging-Jet Regime (low J, high $M_R$) – the jet momentum dominates, crossing the pipe and impinging on the opposite wall, producing intense but localized mixing.

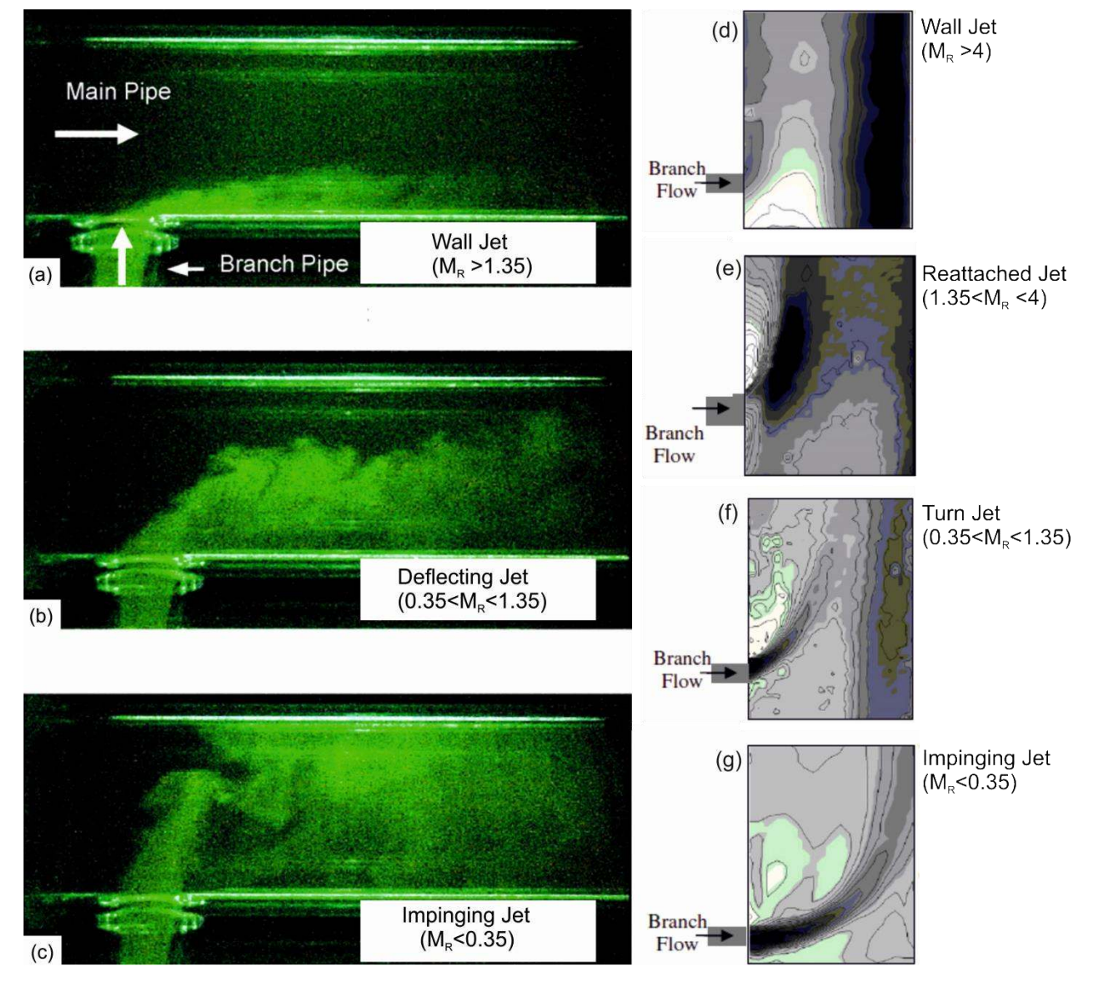
Flow momentum
Figure 2. Flow regimes in T-junctions from Kok \& van der Wal (1996). The authors define $(M_R = \frac{\rho_\text{jet} U_\text{jet}^2}{\rho_\text{main} U_\text{main}^2})$ ; here $(J = \frac{1}{M_R})$, so the horizontal ordering (wall - deflected - impinging) corresponds to increasing jet strength and decreasing ( J ).

To connect these experimental observations with my numerical work, Figure 3 below show COMSOL velocity–magnitude contours and streamlines at two representative conditions:

High J – crossflow-dominated case (N₂ = 3000 sccm, H₂ = 2000 sccm) The jet bends sharply and remains attached to the wall, matching the “wall-jet” behavior seen experimentally.

Moderate J – balanced momentum case (N₂ = 1457 sccm, H₂ = 500 sccm) The jet penetrates into the main stream and rolls up into a kidney-shaped CVP, consistent with the “deflected-jet” regime.

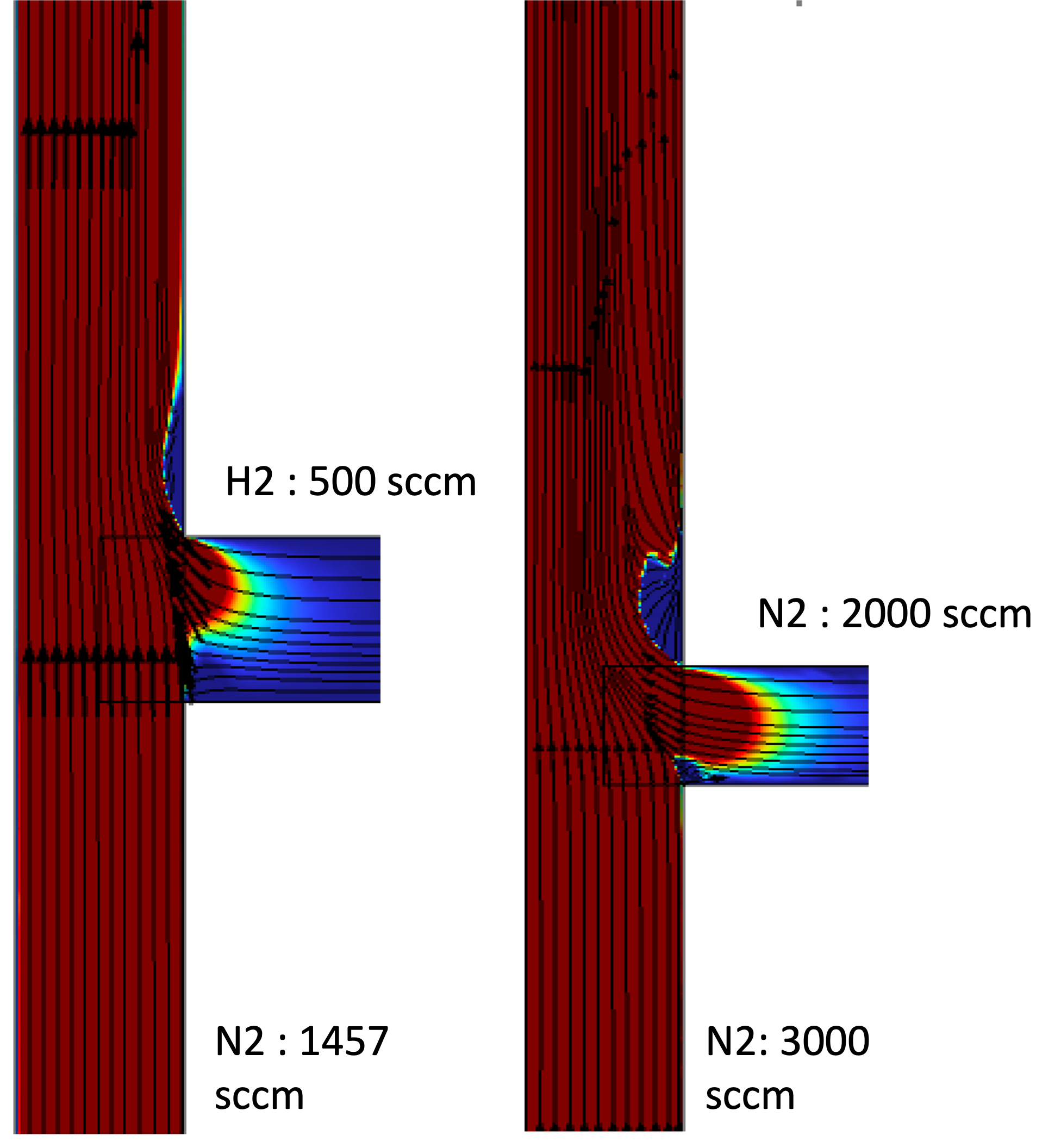
Flow momentum
Figure 3. {High (J)} – crossflow-dominated case (N₂ = 3000 sccm, N₂ = 2000 sccm).
The jet bends sharply and remains attached to the wall, matching the “wall-jet” behavior seen experimentally. {Moderate (J)} – balanced momentum case (N₂ = 1457 sccm, H₂ = 500 sccm).
The jet penetrates into the main stream and rolls up into a kidney-shaped CVP, consistent with the “deflected-jet” regime.

⚠️ Note: My COMSOL simulations were parameterized by jet-to-crossflow velocity ratios, not explicit momentum ratios. Still, the qualitative transitions align directly with the regimes mapped in literature against (J).

Mixing Metrics: From CV to Mixing Length

While the flow regimes describe how the jet and crossflow interact, the actual efficiency of mixing can be captured more quantitatively.
A common measure is the \textbf{Coefficient of Variation (COV)}, which compares the standard deviation of concentration to its mean value:

\[\text{COV} = \frac{\sigma_C}{\overline{C}} = \frac{\sqrt{\langle (C - \overline{C})^2 \rangle}}{\overline{C}}\]

Here, (C) is the local concentration, $(\overline{C})$ is the mean value across the cross-section, and $(\sigma_C)$ is the standard deviation.
A perfectly mixed flow has COV = 0, while a mixture is considered ``uniform’’ when COV ≤ 0.05 (Sun et al., 2020).

In a T-junction, (COV) decreases gradually along the main channel as the jet entrains and diffuses into the crossflow.
The rate at which this happens depends strongly on the momentum ratio (J):

High (J) – the crossflow dominates, and the jet hugs the wall. Mixing is slow and requires a long downstream length. Moderate (J) – the jet and crossflow have comparable momentum. The CVP folds the interface efficiently, leading to faster homogenization. Low (J) – the jet dominates and penetrates fully across the pipe, resulting in rapid but locally intense mixing.

Hydrogen blending studies show a similar dependence on momentum ratio (Tian et al.).
At 10% H₂, the required mixing length is roughly (100D), while at 25% H₂ it drops to about (21D).
This same trend appears in my COMSOL simulations — stronger jets (lower (J)) mix quickly, whereas crossflow-dominated configurations (higher (J)) require a much longer channel to achieve uniformity.

Design Lessons

Momentum ratio is the master knob. More than Reynolds number or angle tweaks, the momentum balance sets the mixing regime.
Trade-offs are fundamental. Impingement → fastest mixing, but highest ΔP and strongest thermal fluctuations (Thermal mixing in T-junctions).
Geometry tweaks help, but momentum dominates. Injection angle, upstream elbows, and branch protrusion improve efficiency (Ansah et al., 2024).
Density differences complicate things. Light gases stratify unless jet momentum is sufficient (Mixing of dense/light gases model).

Closing Thoughts

A T-junction is deceptively simple but hides rich vortex dynamics.
By reframing the momentum ratio as crossflow vs. jet, the regimes become intuitive: the outcome depends on which stream “wins” the momentum battle.

Even though my COMSOL simulations did not directly calculate (J), the velocity-ratio sweeps clearly reproduce the same qualitative regimes reported in literature - making the physics vivid and bridging numerical work with experimental observations.